Mysterious equality

And now, here’s the next question: how on earth is it that π² is approximately equal to g? You might say that such questions aren’t asked in polite society. First of all, they aren’t exactly equal. There’s already a difference in the second decimal place. Secondly, π is a dimensionless number, while g is a physical quantity with its own units.

And yet, no matter how you look at it, this can’t just be a simple coincidence.

Not as simple as it seems

Let's start by taking a close look at the right side. The value 9.81 is in m/s². But these are far from the only units of measurement. If you express this value in any other units, the magic immediately disappears. So, this is no coincidence—let's dig deeper into the meters and seconds.

What exactly is a "meter," and how could it be related to π? At first glance, not at all. According to Wikipedia, a "meter is the distance light travels in a vacuum during a time interval of 1/299,792,458 seconds." Great, now we have seconds involved—good! But there's still nothing about π.

Wait a minute, why exactly 1/299,792,458? Why not, for example, 1/300? Where did this number come from in the first place? It seems we need to delve into the history of the unit of length itself to understand this better.

A standard for every honest merchant

In the past, people didn't bother much with standards: they only cared about what was convenient for measurement. For example, why not measure length in human cubits? It might not be precise, but it was cheap, reliable, and practical. And the fact that everyone's cubits were of different lengths? Sometimes that was even useful. If you needed to buy more cloth, you'd call the tallest person in the village and have them measure the fabric with their cubits.

Later on, of course, people began thinking about standardization. They started creating various standards. But this turned out to be inconvenient and cumbersome: you couldn't always run to a single standard for measurement. So, copies of the standards began to appear. And then copies of the copies...

Serious people decided that such chaos was hindering serious business, so they set a goal: to come up with a definition of a unit of length that wouldn't depend on any arbitrary standards. It should only depend on natural constants, so that anyone with some basic tools could reproduce and measure it.

Bright dreams of standardization and insidious gravity

A "standard-free" definition for the meter was actually proposed back in the 17th century. The Dutch mechanic, physicist, mathematician, astronomer, and inventor Christiaan Huygens suggested using a simple pendulum for this purpose. You take a small object and suspend it on a string. The length of the string should be such that the pendulum completes a full oscillation (returns to its original position) in exactly two seconds. This length of string was called the "universal measure" or the "Catholic meter." This length differed from the modern meter by about half a centimeter.

The proposal was well-received and adopted. However, problems soon arose. First, Huygens was dealing with what he called a "mathematical pendulum." This is a "material point suspended on a weightless, inextensible string." A material point and a weightless string are hardly the simple tools that every merchant would have on hand.

Second, it was quickly discovered that the length of the pendulum's string varied in different parts of the Earth. Gravity cunningly decreased as one approached the equator and did not cooperate with humanity's bright dream of standardization.

An astonishing equation

But let’s return to our mysterious equation. To find the period of small oscillations of a mathematical pendulum as a function of the length of the suspension, the following formula is used:

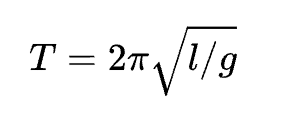
And here it is—our π! Let's substitute the parameters of Huygens’ pendulum into this formula. The length of the string l in Huygens' pendulum equals 1. The T - oscillation equals 2. Plugging these values into the formula, we get π²=g.

So, have we found the answer to our question? Well, not quite. We already saw that the equality is only approximate. It doesn’t feel right to equate 9.87 and 9.81 exactly. Does this mean that the meter has changed since then?

With revolutionary greetings from France

Yes, indeed, it did change! This occurred during the reform of the units of measurement initiated by the French Academy of Sciences in 1791. Intelligent people suggested maintaining the definition of the meter through the pendulum, but with the clarification that it should specifically be a French pendulum—at the latitude of 45° N (approximately between Bordeaux and Grenoble).

However, this did not sit well with the commission in charge of the reform. The problem was that the head of the commission, Jean-Charles de Borda, was a fervent supporter of transitioning to a new (revolutionary) system of angle measurement—using grads (a grad being one-hundredth of a right angle). Each grad was divided into 100 minutes, and each minute into 100 seconds. The method of the seconds pendulum did not fit into this neat concept.

The true and final meter

In the end, they successfully got rid of the seconds and defined the meter as one forty-millionth of the Paris meridian. Or, alternatively, as one ten-millionth of the distance from the North Pole to the equator along the surface of the Earth’s ellipsoid at the longitude of Paris. This measurement slightly differed from the "pendulum" meter. The commission, without false modesty, dubbed the resulting value as the "true and final meter."

The idea of a universal standard accessible to everyone waved goodbye and faded into the sunset. Need an accurate standard for the meter? No problem! All you have to do is measure the length of a meridian and divide it by a few million. By the way, the French actually did this—they physically measured a portion of the Paris meridian, the arc from Dunkirk to Barcelona. They laid out a chain of 115 triangles across France and part of Spain. Based on these measurements, they created a brass standard. Incidentally, they made a mistake—they didn't account for the Earth's polar flattening.

Conclusion

Let's return to our equation once again. Now we know where the inaccuracy comes from: π² and g differ by about 0.06. If it weren't for yet another attempt to reform and improve everything, we would now have a slightly different value for the meter and the elegant equation π² = g. Later, scientists did return to defining the meter through unchanging and reproducible natural constants, but the meter standard was no longer the same.